Peixuan Zhang
PhD student
Penn State University
Biography
Peixuan is a fourth-year Phd student at Penn State University, working with Dr. Uday V. Shanbhag. She is a driven, passionate, and hard-working Ph.D. student conducting multiple research projects on Stochastic Optimization, Convex optimization and Machine Learning.
Interests
- Stochastic Optimization
- Convex Optimization
- Chance-constrained Optimization
- Machine Learning
- Statistical Learning
Education
PhD in Industrial Engineering & Operations Research, 2020 - Now
Penn State University
MS in Statistics, 2017 - 2020
University of Minnesota
BSc in Mathematics, 2013 - 2017
Dalian University of Technology
Skills
Matlab
90%
Python
90%
R
90%
Statistics
100%
HPC
50%
SQL
50%
Experience
Research Assistant
Penn State University
Working on Stochastic optimization problems with compositional constraints or probabilistic constraints.
Graduate research intern
National Renewable Energy Laboratory
Responsibilities include:
- Investigated Optimal Transmission Switching problems with the AI, Learning Intelligent Systems Group at NREL.
- Built benchmarking models for Mixed Integer Nonlinear Problems in Julia with HPC system.
- Compared different MINLP solvers including BOMIN, COUENNE, SHOT, Juniper on instances from PGlib.
- Prepared conference paper as collaborating author.
Survey Researcher Internship
Public Health Depatment at Hennepin County
Responsibilities include:
- Provided an independent evaluation of non-response bias in a survey analysis of the SHAPE project, a population health data survey program to improve community health and achieve health equity for the community.
- Conducted data analysis on over 11,143 survey responses and estimated the nonresponse bias by using both R and SPSS.
- Improved the survey design for corresponding SHAPE project efforts by supplementing questionnaire enhancements for production of higher quality quantitative data.
Projects
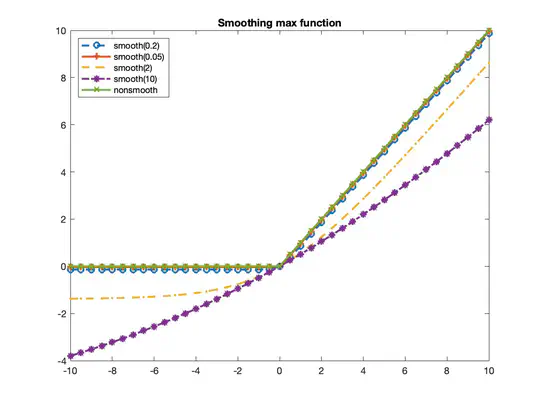
*
We focus on developing an Augmented Lagrangian Method (ALM) frame- work for resolving nonsmooth convex optimization problems. The problem of interest is formulated as follows.
$\min_{\mathbf{x}\in\mathcal{X}} f(\mathbf{x}) \quad \text{subject to} \quad g(\mathbf{x}) \leq 0$
Machine learning techniques to predict opioid misuse
Recent Publications
Quickly discover relevant content by filtering publications.
Contact
Please leave me a message here ~